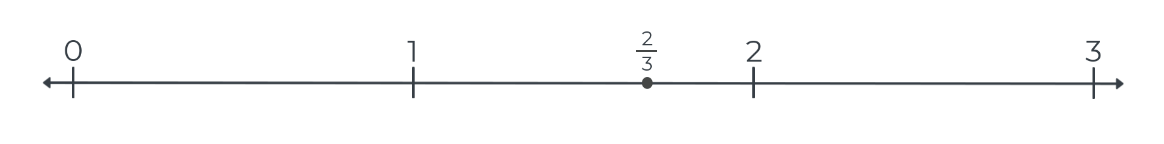Number Line Talk, Tasks, and Practice Pages

NLT Video 3.5 A1 — Measure to Plot and Label Fractions on Number Lines

NLT Objectives

This Number Line Talk targets the following essential concepts and strategies:

  • The length of a unit-fraction bar is defined by the number of equal-length bars that measure a distance of 1 on the number line.

  • The numerator of a fraction is the number of unit-fraction bars that measure from zero to a given point. The denominator of that fraction is the number of unit-fraction bars that measure from zero to 1.

  • Two numbers that measure from zero to the same point on a number line are equivalent.

Next NLT

Number Line Talk — Video

NLT Video 3.5 A1 — Measure to Plot and Label Fractions on Number Lines

Video Overview and Instructional Notes

Click on the image to download a PDF.

The Video Overview and Instructional Notes outline the instructional highlights of this Number Line Talk and lists the essential strategies and concepts that are introduced or reviewed. In addition, video pause points with instructional notes identify important representations, strategies, and concepts and offer suggestions for leading the Challenge discussions with students.

VOIN for Number Line Talk 3.5 A1

Materials List for Number Line Talk

Number Line Talks can be implemented with students using one of the following:

  1. Online interactive Number Line Measurement Tool

  2. Magnetic whiteboard manipulatives from Basic Fraction Number Line Kit

  3. Printable whiteboard manipulatives with strips of adhesive magnets cut from a sheet.

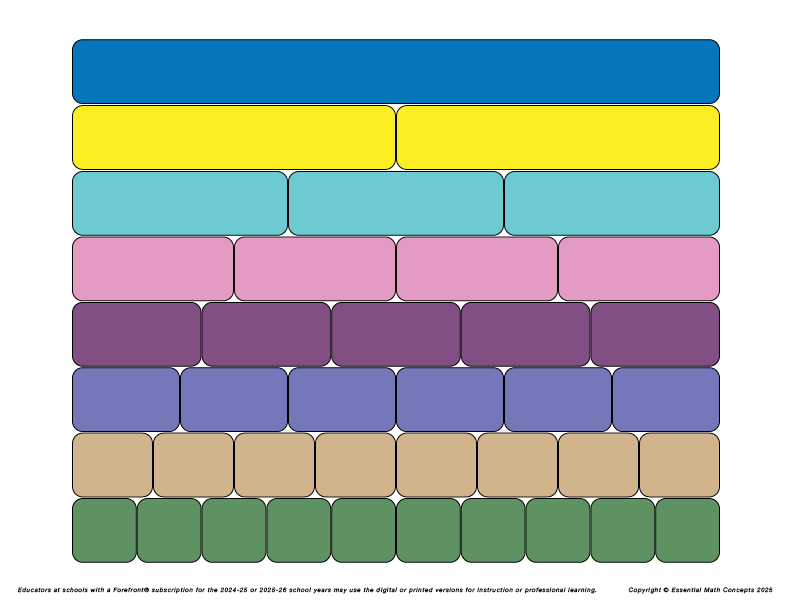
The following number line segments and measurement bars are used in this Number Line Talk if you are using magnetic whiteboard manipulatives instead of the online interactive NLMT.

These resources are available in the Basic Fraction Number Line Kit for magnetic whiteboards, which can be purchased on this website. Printable versions of the bars and fraction strips can be downloaded by clicking on the links below.

NLT Materials List: Measurement Bars and Fractions Strips

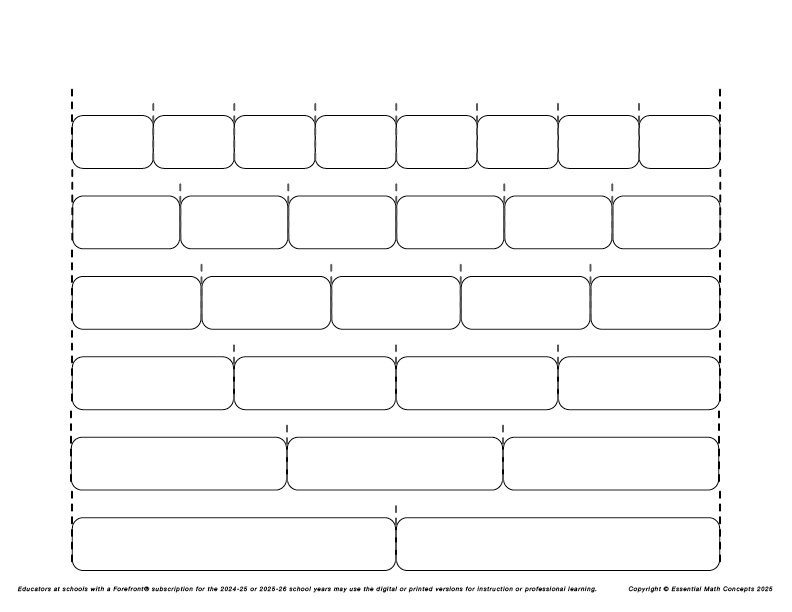
PDFs for Printable Whiteboard Manipulative Kit

Print these PDFs on white card stock. Print two copies of the fraction bars page. Then, use an accurate paper cutter to cut out the individual unit fraction bars and whole fraction strips. Finally, cut short strips of adhesive magnetic sheets and mount them on the back of each bar and strip. Use a long enough piece of adhesive magnet to firmly hold the bar in place on a whiteboard. Note that adhesive magnetic sheets can be purchased online or through an arts supply vendor.

Note: Once you have drawn a 48-inch line on a whiteboard, use one of the fraction strips to measure and draw the tick marks. This will ensure that the fraction bars and strips measure accurately on the number line.

Click on the image to download a PDF.

Note that Magnetic Manipulative Kits for number lines can be purchased from Essential Math Concepts. These kits include foam measurement bars that are easy for students to line up end-to-end to accurately measure fractions on number lines. These kits also include magnetic number line strips that allow teachers to quickly and accurately build a number line on a 48-inch whiteboard.

The printed versions of the measurement bars are more difficult to line up accurately below a number line, but the cost of the kit is negligible.

Conceptual Overview

This Number Line Talk introduces unit-fraction-bars to measure and label points that fall between whole numbers on number lines. The length of a unit-fraction-bar is defined by the number of equal-length bars that measure from zero to 1. In addition, unit-fraction-bars will be used to label fractions greater than one and to identify fractions that are equivalent to whole numbers.

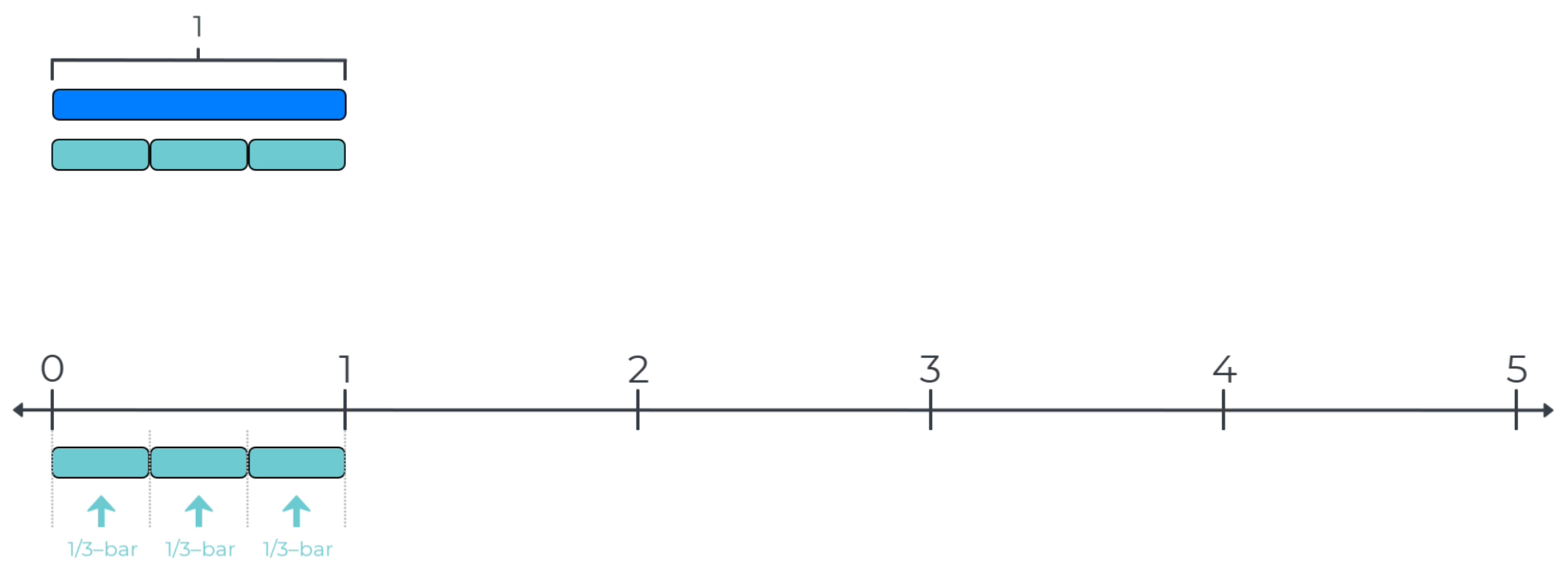
Unit-fraction-bars are sets of equal-length bars that measure a length of 1. In the example below, three equal-length bars measure the same length as a 1-bar in the measurement key. So, each of these unit-fraction-bars measures a length of 1/3.

On the number line, one 1/3-bar measures from zero to 1/3, and two 1/3-bars measures from zero to 2/3.

By definition, three 1/3-bars or 3/3 measures from zero to the tick mark for 1. Numbers that measure to the same point on a number line are defined to be equivalent.

Unit fraction bars are also used to measure fractions greater than 1.

Because the standard manipulative kit only contains enough unit fraction bars to measure from zero to 2 on this number line, fraction strips in the manipulative kit are used to measure fractions greater than 2. In the example below, the fraction strip is used to skip count to measure 3/3, 6/3, and 9/3. Then, one additional 1/3-bar measures to 10/3. Note: Only print two copies of the fraction bars if you use the printed versions of the manipulative kit. This will necessitate the use of the fraction strip to apply a skip-counting strategy, which builds a foundation for

Note: Only print two copies of the fraction bars if you use the printed versions of the manipulative kit. This will require students to use the fraction strip to skip-count by fractions equivalent to whole numbers. Repeatedly applying this skip-counting strategy will help prepare students to understand strategies for converting mixed numbers to fractions and vice versa.

Related Professional Learning Videos

PL Video NLT 3.5 A — Measure to Plot and Label Fractions and Mixed Numbers on Number Lines

Click on image to download PDF

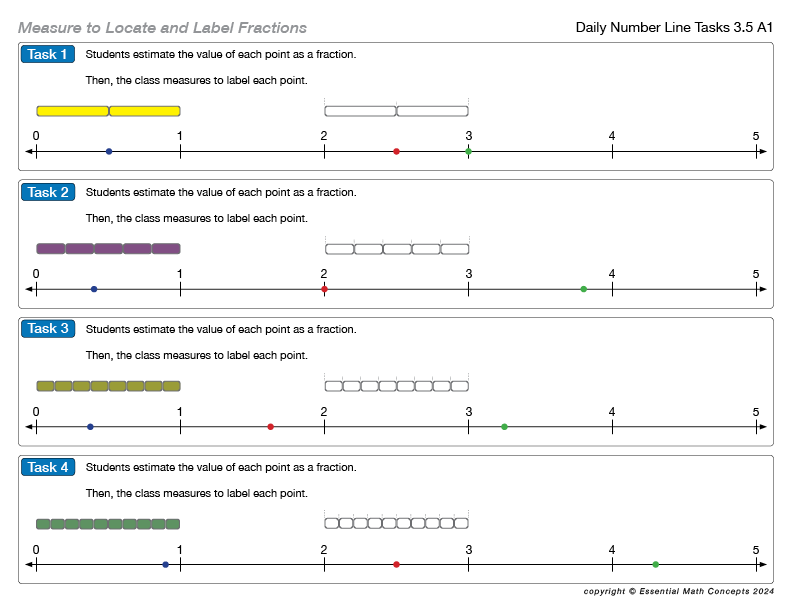
NLMT — Daily Number Line Tasks

Use the online interactive Number Line Measurement Tool to display each task. After students estimate the value of each point on the line, they can use the NLMT to share their measurement strategies with the class.

Daily Number Line Tasks

The Daily Number Line Tasks can be represented on the whiteboard so students entering the classroom can review and complete the task. Then, to start class, students can share strategies to measure and label points on the number line. This brief activity allows teachers to review important concepts and strategies introduced in the Number Line Talk Video and applied on the Number Line Practice Pages.

Daily Number Line Tasks—3.5 A1

Number Line Practice Pages

The Number Line Practice Pages challenge students to apply the concepts and strategies that were introduced in the Number Line Talks and reviewed in each Daily Number Line Task.

Measurement-Bar Ruler

Students will use the rulers to complete some Number Line Practice Pages. A PDF of a set of rulers is included as the last page of the PDF for the Practice Pages. Print these rulers using the same printer/copier used to print the Practice Pages. Then, use a paper cutter to cut out and trim the rulers. This process ensures that the printed size of the rulers and Practice Pages are the same so that rulers measure accurately on the Practice Pages.

PDF of Number Line Practice Pages and Printable Rulers —NLT 3.5 A1

Click on image to download PDF

Apply Strategies and Concepts from Number Line Talk

Number Line Talk — Application 1

Plot and Compare Unit Fractions

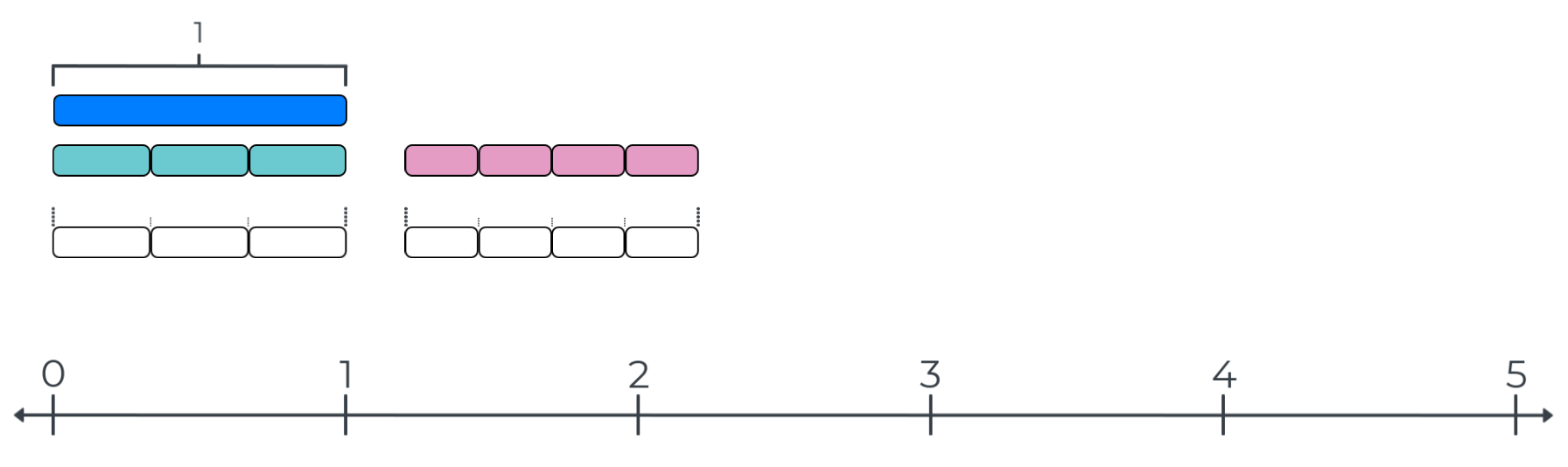
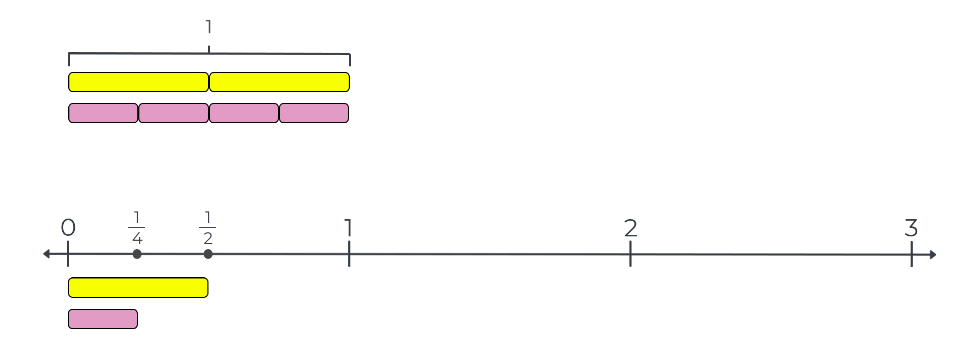
A common student misconception when representing unit fractions on number lines is to plot unit fractions with greater denominators further to the right than fractions with lesser denominators (see diagram below). This Number Line Talk Application challenges students to apply measurement bar strategies that they learned from the Number Line Talk to plot and label unit fractions. Then, students are asked to compare where unit fractions with different denominators are plotted on the same line. Finally, students are challenged to apply what they have learned about the location of unit fractions to estimate the location of unit fractions with larger and larger denominators. Note that students can also be challenged to explain whether any unit fractions are located between the point of 1/2 and 1 (or greater than 1) on the number line.

Student Misconception when Plotting Unit Fractions

This application problem is an opportunity for students to compare the location of different unit fractions on a number line. Then, students can be challenged to make mathematical statements about the locations of different unit fractions. For example, fractions with greater denominators are closer to zero on the number line. Finally, students can be challenged to justify these mathematical statements using concepts and strategies that they learned in the Number Line Talk.

For example, the following statement, "the point for 1/4 is closer to zero than the point for 1/2," can be justified by explaining that a 1/4-bar is shorter than a 1/2-bar because four 1/4-bars and two 1/2-bars measure the distance between zero and 1 on a number line. So, one 1/4-bar will measure to a point closer to zero than one 1/2-bar. Notice that this reasoning builds directly out of the naming strategy for unit-fraction bars and the basic strategy used to measure to fractions on a number line.

Representing Unit Fractions Using Measurement Bar Strategies

Number Line Talk — Application 2

Compare Fractions Less Than and Greater Than 1

NLMT — NLT Application 1

Use the online interactive Number Line Measurement Tool to complete this NLT Application activity with a small group or class of students.

Each NLT Application extends concepts and strategies introduced in this Number Line Talk to address common student misconceptions or to introduce related essential concepts and strategies.

Students can also apply what they have learned in this Number Line Talk to reason about the numerators and denominators of fractions that are less than and greater than one. This Number Line Application is motivated by students incorrectly plotting points such as 2/3 between the tick marks for 2 and 3 on a number line.

Student Misconception when Plotting Fractions

This application problem is an opportunity for students to plot a set of fractions that are less than and greater than one. Then, students can be challenged to compare the numerators and denominators of the plotted fractions. Once again, students can be challenged to extend these comparisons to make mathematical statements, such as “fractions that are greater than 1 have numerators that are greater than the denominator.”

Then, students can be challenged to justify these mathematical statements using strategies and concepts from the Number Line Talk. For example, the denominator of a fraction is defined by the number of unit fraction bars that measure from zero to one. Since fractions greater than 1 will always be measured with a number of unit fraction bars that is greater than the number that measures to 1, the numerator of these fractions will always be greater than the denominator.

NLMT — NLT Application 2

Use the online interactive Number Line Measurement Tool to complete this NLT Application activity with a small group or class of students.