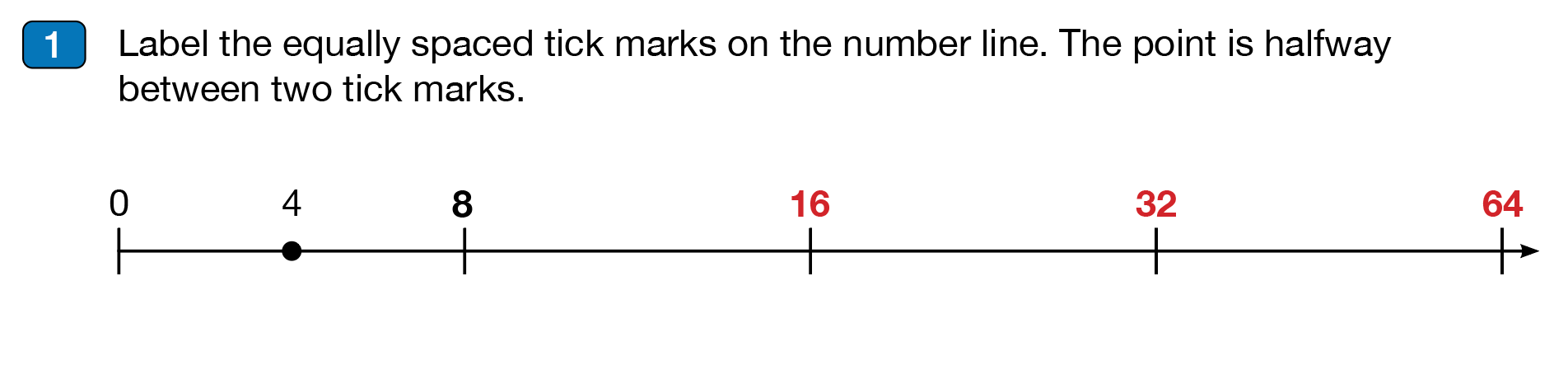Let’s do some math!
Assess Basic Number Line Strategies
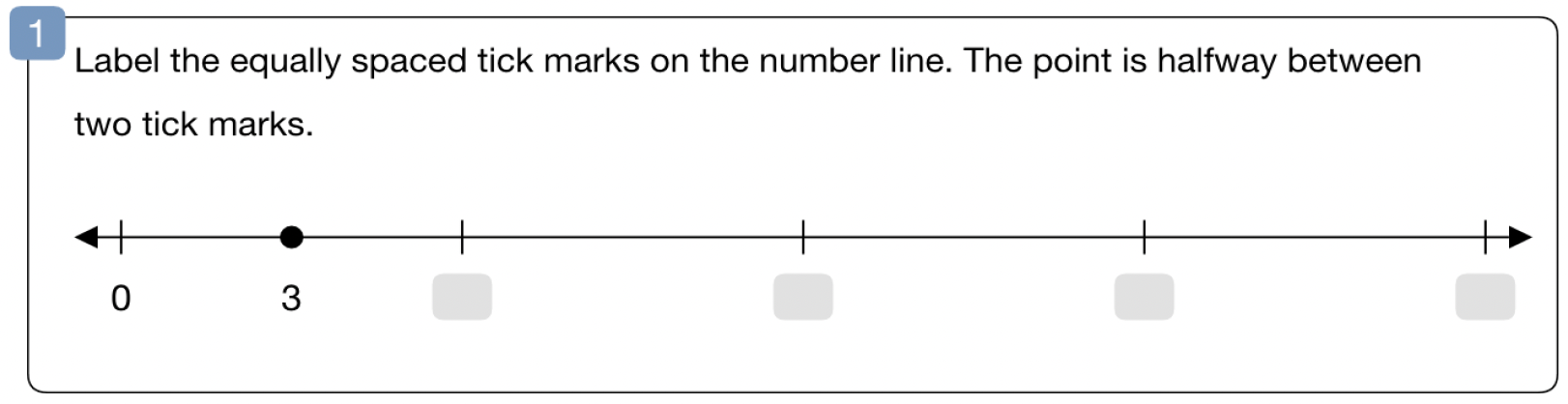
Try this problem with your students
Give this problem a try with your students in grades 3-8. Read the problem as-is and ask students to label the tick marks on the number line. If students ask for clarification, point out that this number line has two labeled numbers and that they should use this information to label the value represented by each tick mark.
Subsequent posts below will address students’ understandings and misconceptions of number lines and diagrams that include them. There is also a video that explores how to introduce students to basic measurement strategies on number lines.
Multiple copies of this question are organized on a printable PDF. Click on the image below and enter the password EMC to view and print this PDF. Once the PDF page is printed, use a paper cutter to cut out the questions for individual students. Note that this is Question 1 on the Screening Assessment for Basic Number Line Strategies, which is available in a post further down on this webpage.
EMC Video — Basic Number Line Measurement Strategies
Did some (or many) of your students mislabel the tick marks in Problem 1? If they did, watch the video below to learn more about the basic measurement strategy for number lines and to explore how you can introduce this foundational number line strategy to students.
What were students thinking?
So here are a few of the incorrect answers to Problem 1 that we have seen in grades 3-8.
The most basic incorrect strategy is demonstrated by the student's response below. This student likely sees number lines as a diagram that lists the sequence of whole numbers, which is how number lines are first introduced to students in kindergarten and 1st grade. So, the student extends the pattern of whole numbers from 4 to 5, 6, 7, and 8, to label the tick marks.
Another incorrect strategy misapplies a doubling pattern represented by the incorrect labels below
The common theme for each incorrect strategy is that students are searching for a pattern to extend. And, they think that points and tick marks on number lines are correctly labeled if the numbers form a pattern. This is why many students incorrectly say that all of these strategies are correct because they recognize the pattern and think that the pattern makes a labeling strategy correct.
This misconception develops when legitimate skip-counting patterns are used to label equally spaced tick marks, and students are not challenged to label points that break the pattern. This problem breaks the skip-counting pattern and is an opportunity to introduce a foundational number line concept, the basic measurement strategy for number lines. This strategy states that a given distance on a number line, such as the length of a bar that measures from the tick mark for zero to a point representing 4, measures the same distance, a length of 4, when it is moved anywhere else on this number line. This rule for number lines is straightforward for students to understand. And, once they have learned it, they can apply it to justify the location of whole numbers, fractions, decimals, and other rational numbers on number lines.
The previous video demonstrates how measurement bars can be used to introduce this basic measurement strategy and how students can apply this strategy to measure and justify the values of tick marks on this line. So, the basic measurement strategy transforms students’ understanding of number lines from a pattern-seeking task to a task that applies a basic property of number lines, distance corresponds to value, to justify the location of numbers on that line.
The most common incorrect strategy misapplies a skip count pattern represented by the incorrect labels below. Once again, the student is looking for a pattern to extend and label the tick marks. This patterning strategy does not work because the distance between the point for 4 and the tick mark for 8 is not the same as the distance between the equally spaced tick marks.
Assess Basic Number Line Strategies
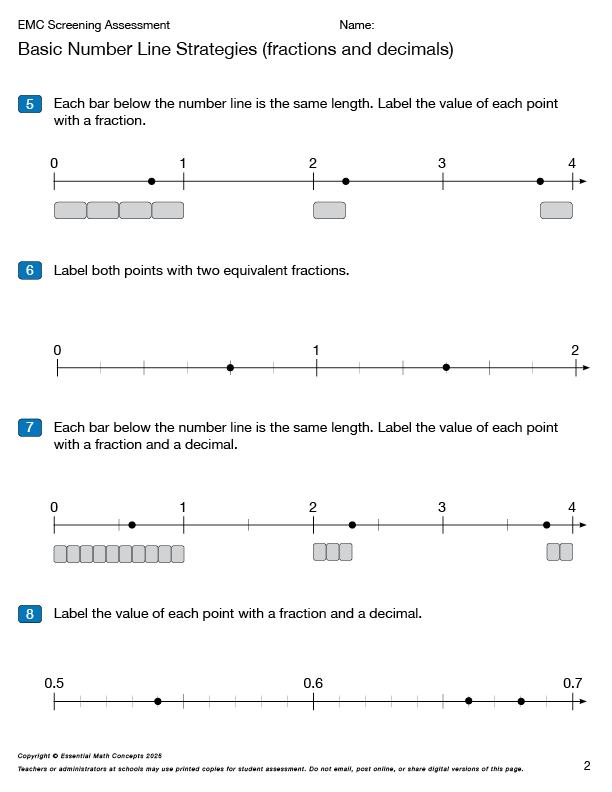
This 8-question screening assessment can be used to identify which basic number line strategies students are bringing with them into middle school. Students will need these number line strategies with whole numbers, fractions, and decimals to be prepared to represent rational numbers on number lines in grades 6 and 7.
Click on the image below and enter the password EMC to view and print these assessment pages.
Apply Number Line Measurement Strategies to Preview a Foundational Middle School Topic — Represent Rational Numbers
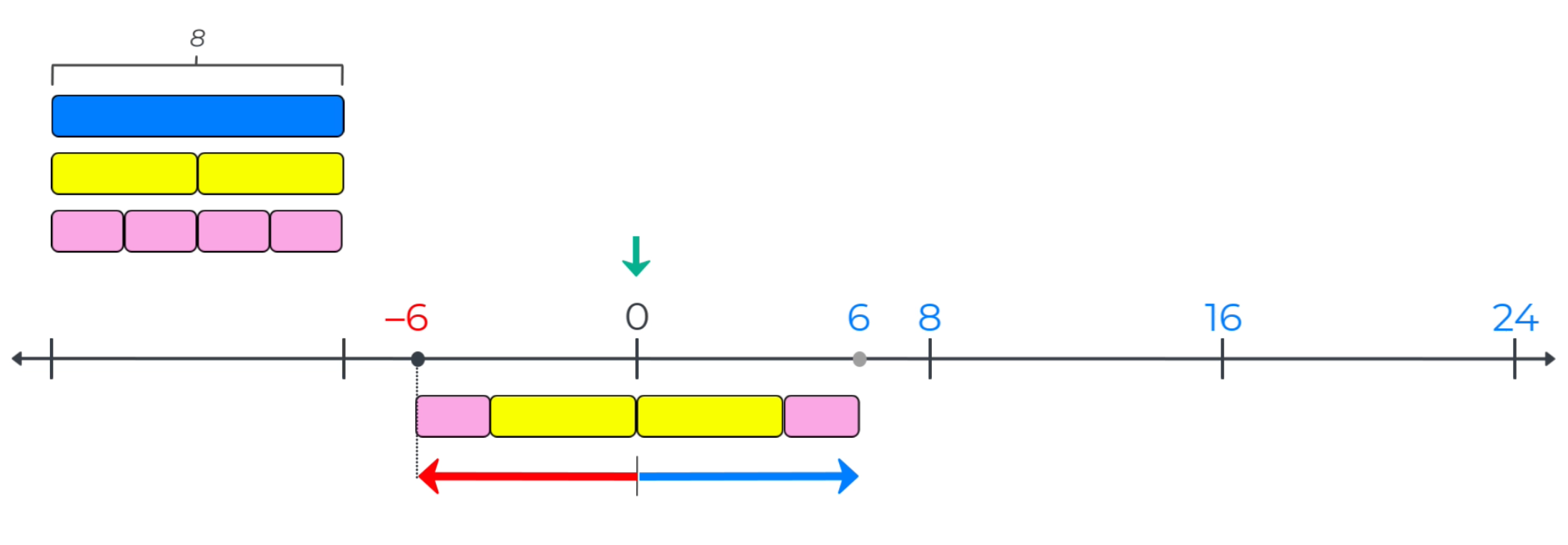
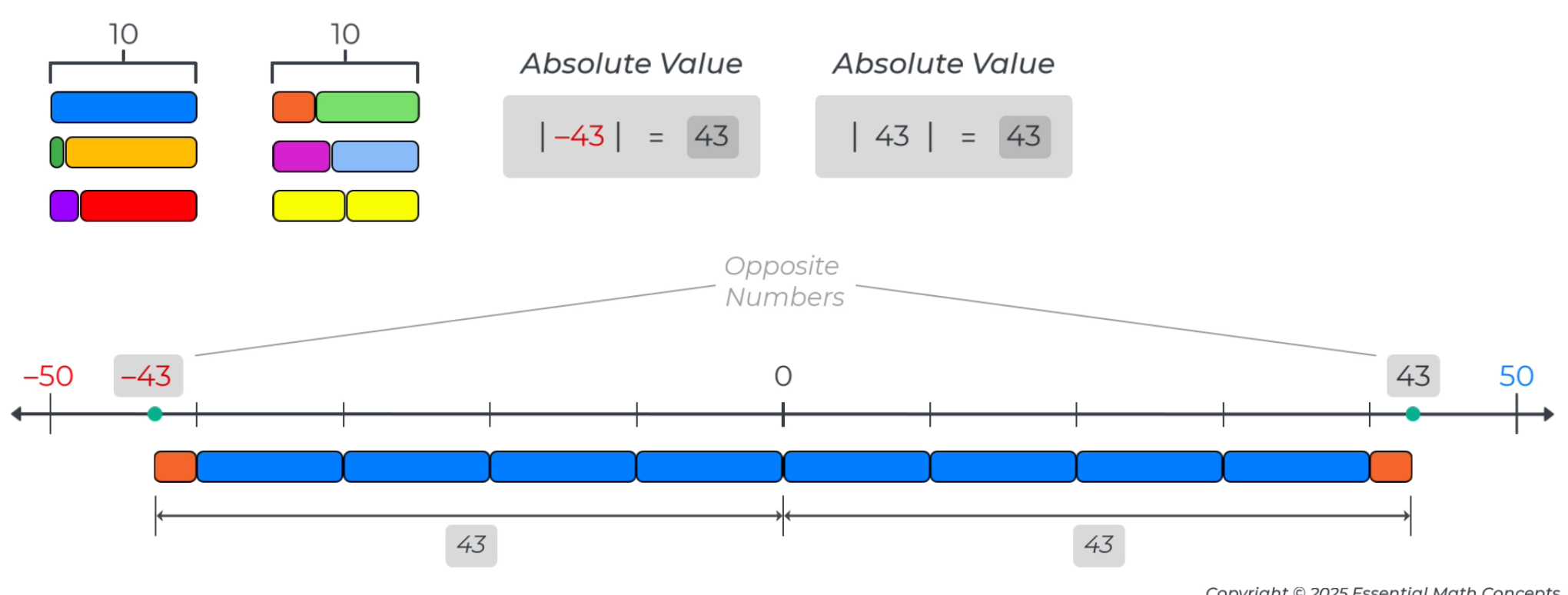
Once students have mastered the use of measurement strategies to locate whole (positive) numbers to the right of zero, negative numbers can be introduced as the reflection of positive numbers across the tick mark for zero.
So, the measurement strategies used to locate and label whole numbers to the right of zero in grades 3-5 are used in grade 6 to plot positive integers to the right and negative integers to the left of zero. In addition, since the bars measure distance to both the right and left of zero, the length of a set of measurement bars used to measure from zero can be introduced as the absolute value of a number.
This application of measurement strategies to represent rational numbers means that assessing students’ knowledge of and ability to use measurement strategies to locate and label whole numbers is a good indicator of student preparedness to learn rational number concepts in Grades 6-8.