Sample PLC Video
Placement in Grades 6-8 Progression
This Grade 6 PLC Video is an introduction to calculating multipliers that relate the two values in each ratio in a set of equivalent ratios. Prior to this video, the sequence of grade 6 PLC Videos explored the use of intuitive and transitional ratio representations and strategies to solve problems and make sense of foundational ratio concepts.
PLC Questions and Prompts
Each PLC Video has an associated set of PLC Questions and Prompts that can be used to structure conversation a professional learning team meeting or a professional development session.
Technical Details
More in-depth issues regarding representations, strategies, and concepts in the progression are addressed in the Technical Details section of this page. The technical topic for this PLC Video focuses on the ordering of quantities in a ratio and the organization of those quantities in a ratio table vs. an algebraic table.
PLC Video
Grade 6 — Ratios
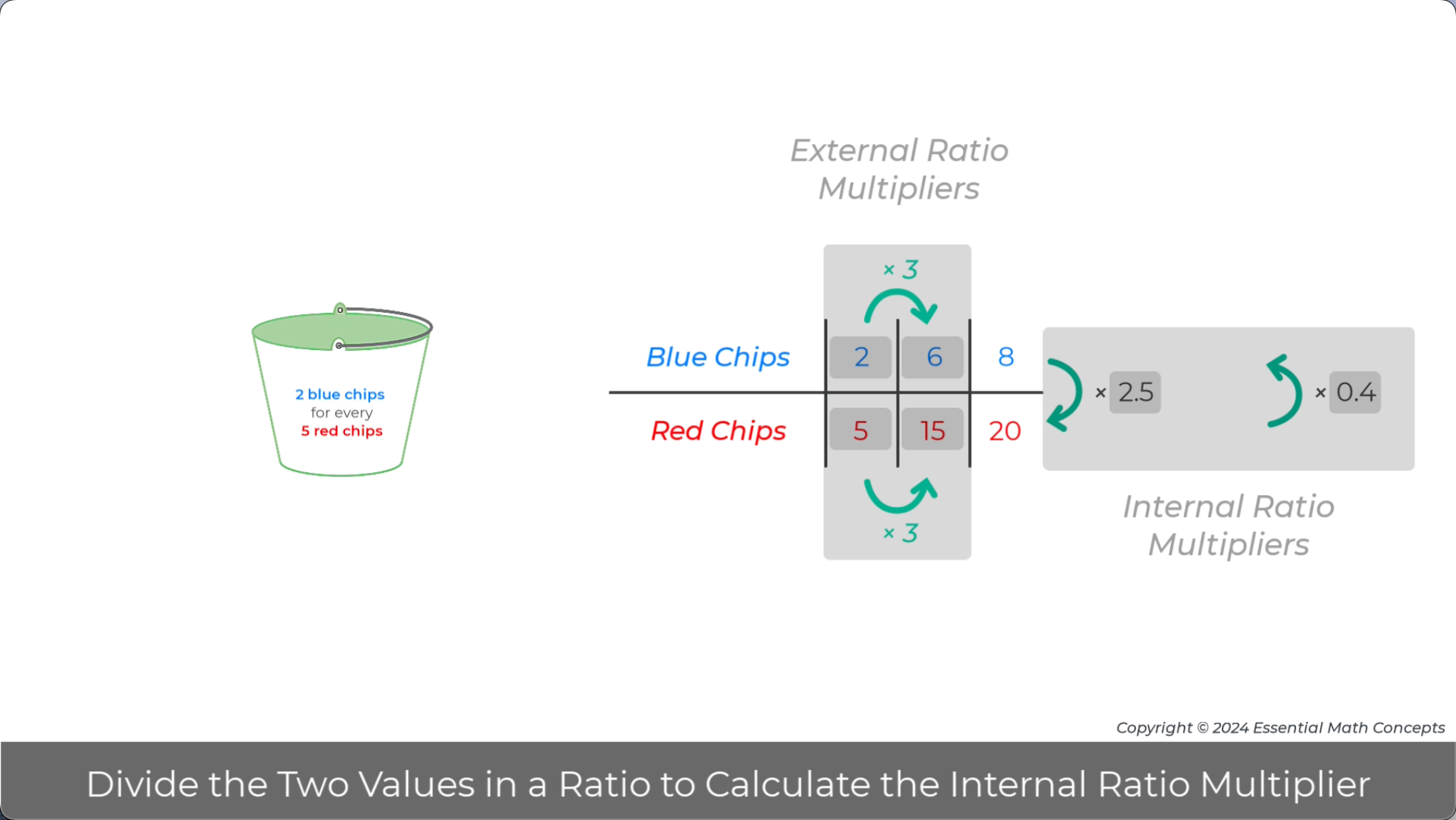
EMC 4A — Divide the Two Values in a Ratio to Calculate the Internal Ratio Multiplier
Grade 6 - Professional Learning Course Videos
PL Video Objectives
Explore how internal ratio multipliers can be introduced by dividing the two quantities in each ratio in a set of equivalent ratios.
Recognize that multiplier arrows are used to represent ratio multiplier relationships in ratio tables.
Implementation Recommendations
PLC Prompts 1-5 can be implemented at a single professional learning team meeting.
PLC Questions and Prompts
This video demonstrates how equivalent ratios in ratio tables are used to generate multipliers that relate the two quantities in each equivalent ratio. Previous professional learning videos explored how rectangular array diagrams are used to generate a set of equivalent ratios.
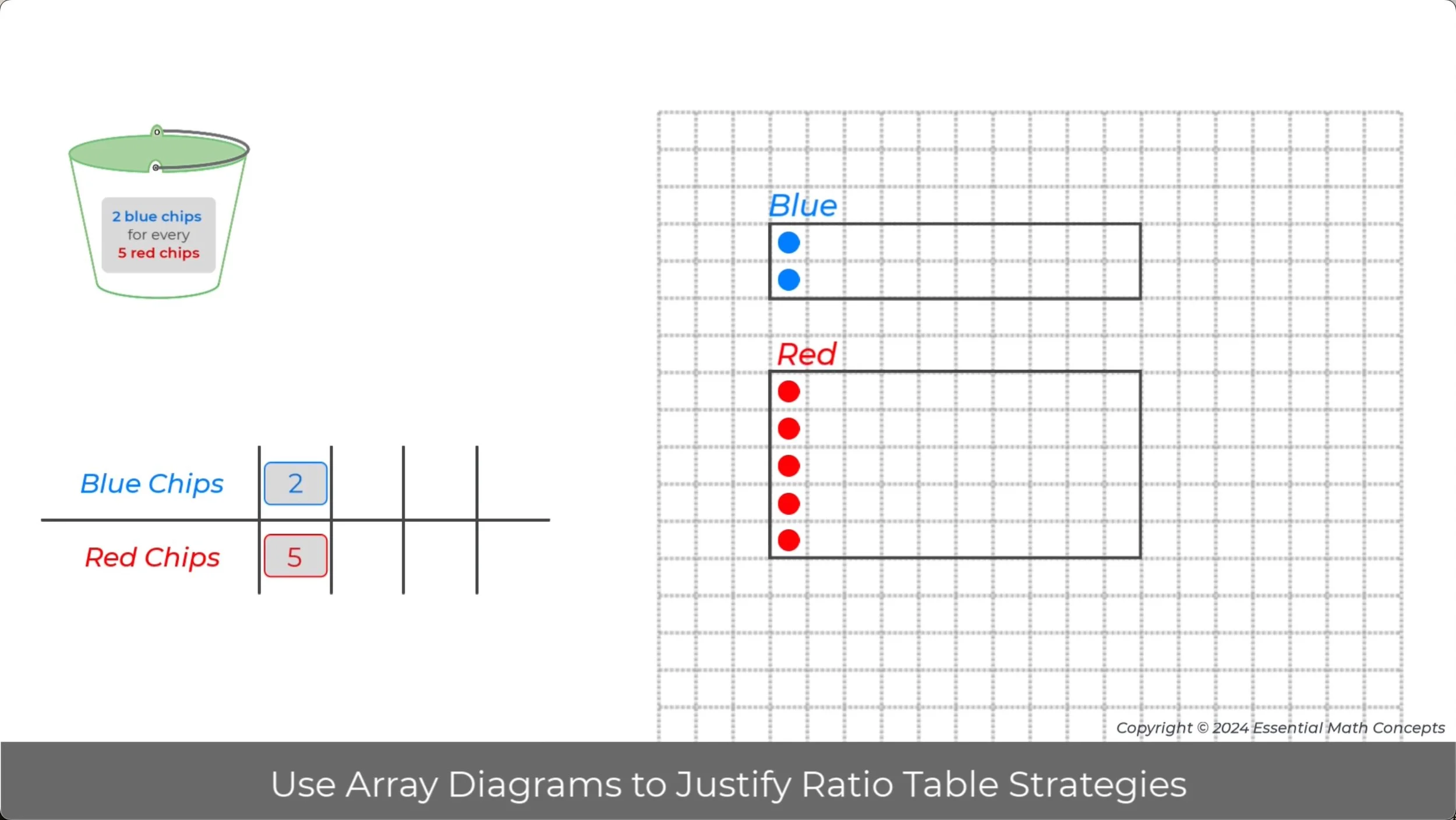
Discuss or demonstrate how students could use rectangular arrays to justify that the ratios in the table are equivalent. An image from a previous PLC Video has been included to facilitate this discussion.
1.
Image - Video Pause Point 0:26
Image from Previous PLC Video
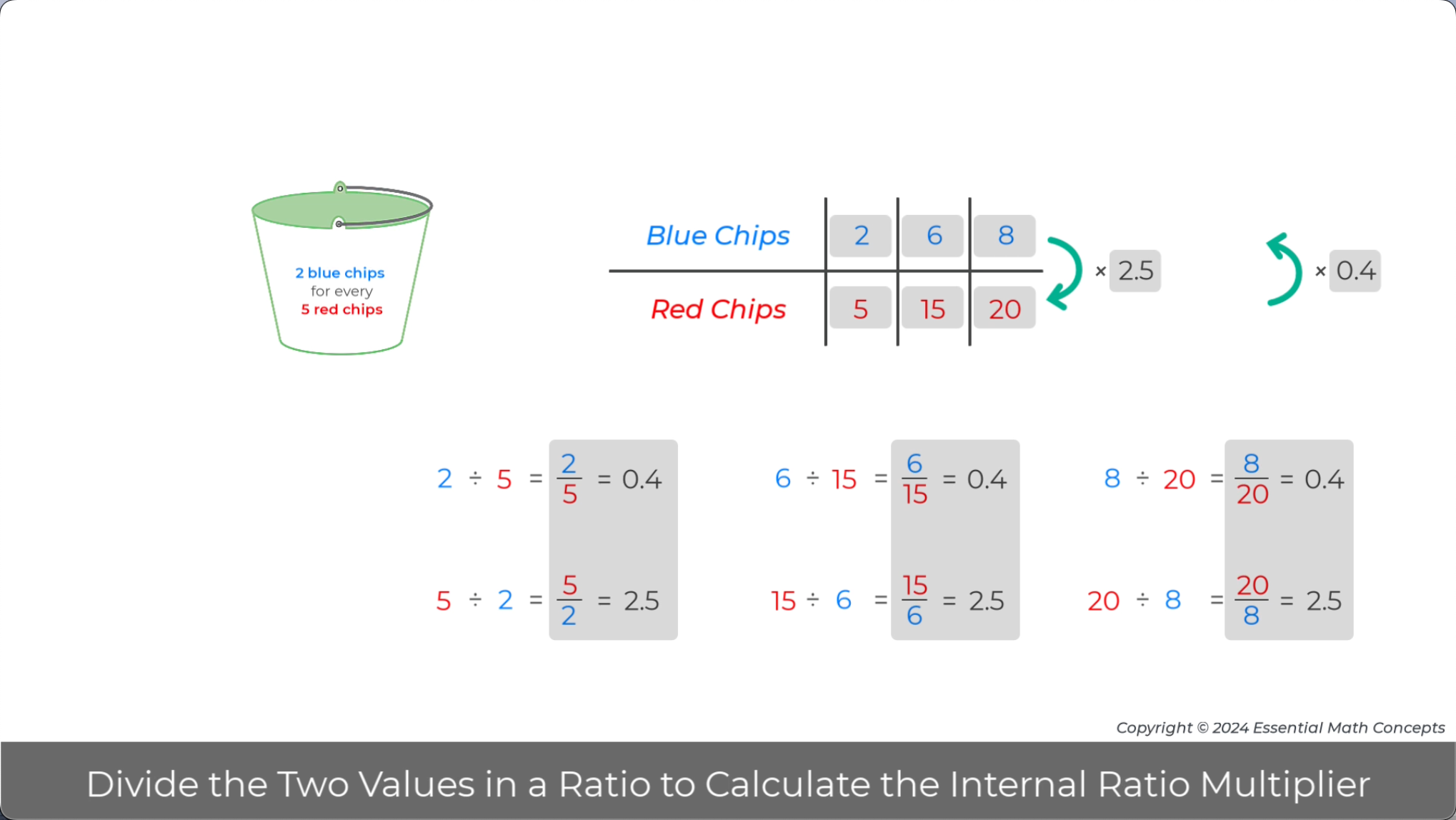
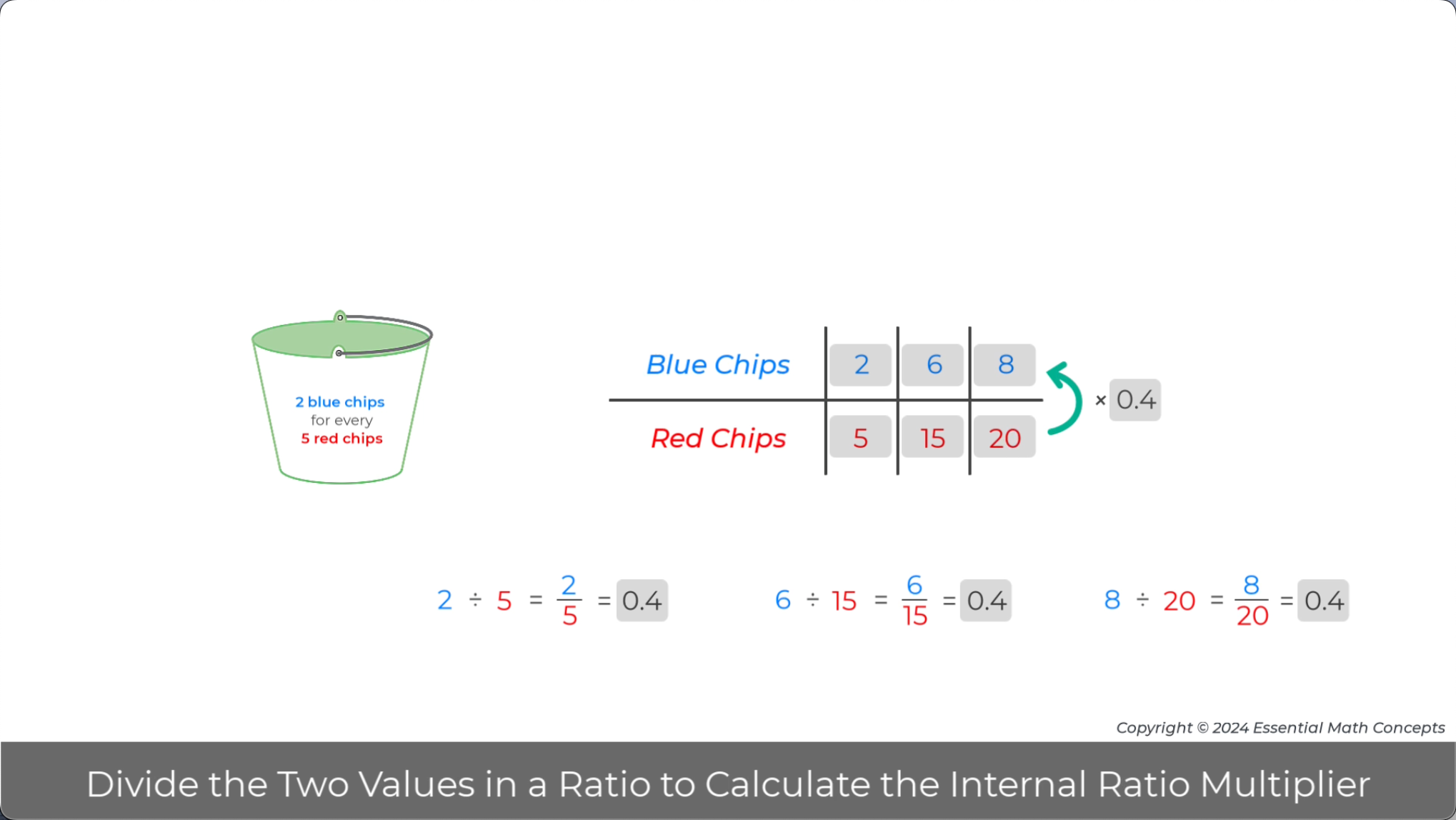
Dividing the two values in each ratio in a set of equivalent ratios always generates a common value. This value is a multiplier that relates the two values in each equivalent ratio.
Discuss how students could use this multiplier to write a multiplication equation for each column (i.e., equivalent ratio) in the table.
How might you frame a question to challenge students to apply this multiplier to generate other ratios that are equivalent to 3 blue chips for every 5 red chips?
2.
Image - Video Pause Point 0:47
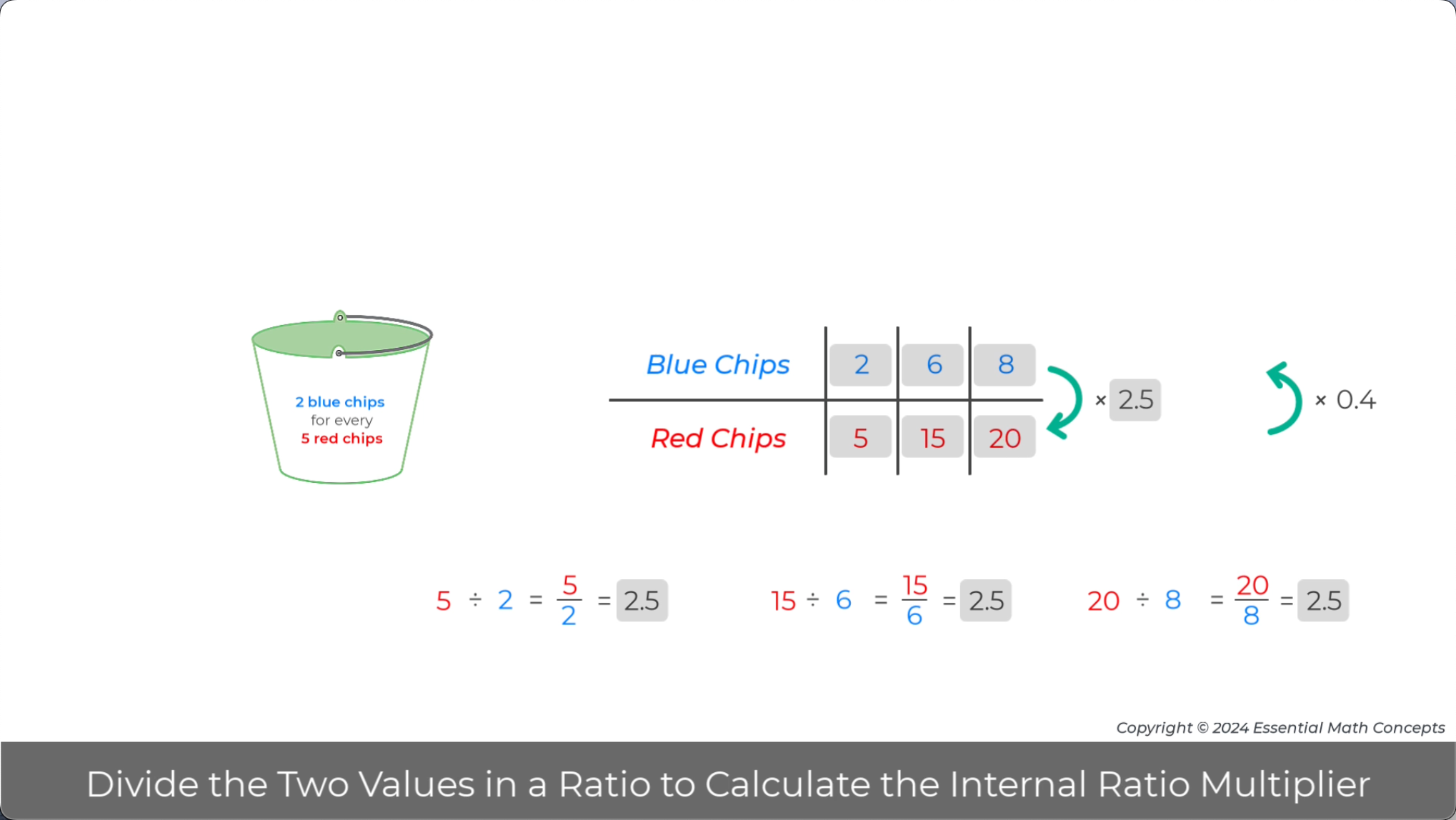
A related multiplier is generated when the order of division is reversed for each equivalent ratio. Once again, students can use this new multiplier to write a multiplication equation for each column and to generate other equivalent ratios.
These internal ratio multipliers can be used to formally define a ratio relationship. Look up the definition of a ratio in your local resources and on the internet. Discuss the strengths and weaknesses of the different definitions.
An intuitive definition of equivalent ratios was introduced using rectangular array diagrams, where a new ratio is equivalent to a given simplified ratio if the new ratio maintains or satisfies the given ratio. Array diagrams allowed students to intuitively apply this definition. How is a ratio definition based on the multiplicative relationships between the two quantities in the ratio more comprehensive than this intuitive definition based on array diagrams?
3.
Image - Video Pause Point 1:09
Dividing and then reversing the order of division, generates a pair of reciprocal multipliers. The fraction versions of the multipliers clearly show that they are reciprocal.
One property of reciprocals is that a number multiplied by its reciprocal equals 1. Explain how students could use this property to check that this pair of multipliers are reciprocals.
In subsequent PLC Videos, division will be applied to reverse the action of a multiplier. For example, if the number of red chips is multiplied by 0.4 to get the number of blue chips then the number of blue chips can be divided by 0.4 to get the number of red chips. Explain how the properties of reciprocals can be used to show that dividing by 0.4 is equivalent to multiplying by 2.5.
4.
Image - Video Pause Point 1:21
Internal ratio multipliers relate the two quantities in a ratio and any equivalent ratio. External ratio multipliers relate the like quantities in two equivalent ratios.
Discuss the similarities and differences between internal and external ratio multipliers.
Explain how the ratio table can help students structure the two different ratio multipliers.
5.
Image - Video Pause Point 1:43
Application and Reflection
Small Group or Classroom Application — Teacher Facilitated Page
This teacher-facilitated Application Page explores the multiplicative relationship between the two quantities in ratio and any equivalent ratio.
Problems 1
Use the array diagram in Problem 1 to complete a set of equivalent ratios in the columns of a ratio table.
Problem 2-3
For Problem 2, ask students to write a numeric division equation for each equivalent ratio in the table. Then, for Problem 3, show students how to use the common value calculated in Problem 2 to draw and label a multiplier arrow for the ratio table in Problem 1. Finally, have students check that the multiplier can be applied to each equivalent ratio in the table. Note: You can provide students with a calculator to keep the focus on the ratio multiplier relationship and not on dividing and multiplying decimals.
Problem 4-5
Repeat the steps from Problems 2-3, but reverse the order of division. Note: The reciprocal relationship between the two ratio multipliers will be explored in subsequent PLC Videos.
Problem 6
Use Problem 6 to challenge students to apply these multipliers to generate other equivalent ratios.
This application page has students justify equivalent ratios using array diagrams and ratio tables. Explain why it is important to have students use less formal strategies to justify equivalent ratios before introducing the formal ratio multiplier strategies.
Explain the difference between internal and external ratio multipliers.
Explain the different ways that students can make sense of the fact that the two ratio multipliers are always reciprocals.
Reflection for PL Course Notebook
Technical Details
The Order of Quantities in a Ratio and the Arrangement of Ratio Quantities in Tables
The two quantities in a ratio have a specific order. For example, a ratio of 2 blue chips for every 5 red chips can be represented using the ratio notation, 2:5. In context, this notation describes the ratio of blue chips to red chips and NOT the ratio of red chips to blue chips.
This ratio can also be represented using fraction notation, 2/5. Notice that this fraction and its decimal equivalent is one of the internal ratio multipliers that relates the number of red chips to the number of blue chips. The reciprocal of this fraction and its decimal equivalent are the reciprocal of the internal ratio multiplier, which relates the number of blue chips to the number of red chips.
When the quantities in a ratio are organized in a ratio table, it is natural to organize the first value in the ratio in the top row and the second value in the bottom row. With this arrangement in the table, the fraction representation of the ratio is the internal ratio multiplier that relates the value in the bottom row to the value in the top row.
On the other hand, when a ratio or rate relationship is represented in an algebraic table the independent variable will be represented in the top row of a horizontal table and in the lefthand column of a vertical table. For example, the constant rate, 6 feet in 2 seconds can be represented in a ratio table where distance in feet is listed in the top row of the table and the time in seconds is listed in the bottom row. In an algebraic or function table, the quantities, or more specifically, the variables, in the two rows would most commonly be switched so time is in the top row. This switch reflects the fact that time, in this context, is usually chosen to be the independent variable. That being said, it is mathematically valid to declare the distance to be the independent variable and time to be the dependent variable so that the original arrangement of variables is correct.
So, to sum up this technical but important topic, the arrangement of quantities in a ratio table (i.e., a table of equivalent ratios) should be based on what makes sense to solve the given problem. When the quantities in a ratio or rate are described as variables in a proportional relationship, the variable identified or declared as the independent variable should be arranged in the top row of a horizontal algebraic table or in the lefthand column of a vertical algebraic table.
In grade 6, students should learn that quantities in ratios and rates have an order, but equivalent ratio quantities can be arranged in a table in a way that makes sense to solve the problem. When algebraic representations of proportional relationships are formalized in grade 7, students should be challenged to identify or declare the independent and dependent variables for a given ratio or rate problem and organize the corresponding algebraic table accordingly.